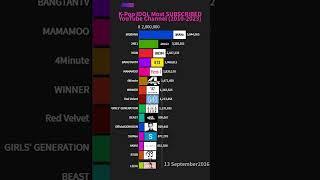
Anna Jencova: Renyi relative entropies and noncommutative Lp spaces
Комментарии:
Anna Jencova: Renyi relative entropies and noncommutative Lp spaces
IMBM İstanbul Matematiksel Bilimler Merkezi
5 Малоизвестных игр жанра Интерактивное Кино!
Сборище Импрессионистов
Отважно, героически, идем до конца: гвардии майор Егор Захаров. #героироссии
Спутник разведчика
Gunjur Leads the growth of peripheries in Bangalore #realestate #bangalorerealestate
Bangalore Real Estate with Abhishek Nipun
ТОП 10 игр ИНТЕРАКТИВНОЕ КИНО
Серёга Гид
Why Chickens Stop Laying Eggs (And What You Can Do About It)
Hobby Farm Guys
Motorcycle Ride - Scone to Gloucester Loop on a Honda NC750X
Honda Africa Twin & NC750x Stuff