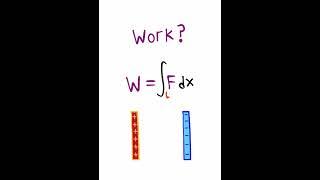MOST Can't Solve It Until College...

What is challenging about that problem? You don't even need the integral since the force is constant both in direction and absolute value.

I knew it when I was in schooll

You can also think of this as simply the fact that work is really how much energy it takes to take a path and that bolt s are simply joules divided by coulombs if you know the units of work volts and coulombs there's no need to even think about the integral

❤ garde

Positive charges will naturally move from a region where they have more potential energy (high potential) to a region where they have less potential energy (low potential)
That is : positive charges tend to move spontaneously from a region of higher electric potential (positive terminal) to a region of lower electric potential (negative terminal). This movement is driven by the electrical force.

Alternate method: Work done by conservative force is (-)ve change in potential energy which is just q times the change in potential

that was the first formula I learnt in potential and capacitance

is it true that education in india being difficult ?? literally any (my positive guess ) 12th grad in india will take less than 3 sec to solve , it doesnt even ask in the classroom level ques , leave the competitve level.

My brain literally about to see this as a capacitor and then find the charges on each side of plates via writing 4 equations for potential data and then find the work by applying field result for a capacitor. Completely skipped that I knew qV 😂

Thank you!!

In highschool we did things like electronic engineering, math and physics

As a industrial chemistry and software engineering major, I'm very drunk and unholy confident in my ability to do this

bruh this is so easy

You must specify work done by whom

emm, I think we have this formula in A level

Wow 😲 superb easy 😊

just learned this around 2 weeks ago. never found a way to integrate calculus into the potential difference though (pun not intended)

Estás despreciando efectos de borde, tu análisis es incompleto

Western education surprises me

Isn't Jules a measure of energy?

Maybe in america, it's for 14yo elsewhere...

isnt E a constant why cant we just integrate the constant

Bruh I did this at alevel

Electrical Potential eneergy= work done/charge...
Class 10 formula.. We can use it too

Two culos?

it’s joules not jewels

...or you could just use W = Vq.

Whats the point of the integral being there

Doesn't the positive plate repel it and the negative attracts so shouldn't the net voltage add. To something like q400V might I say.

bro that's literally the one of the most fundamental equations in electrostatics

This is grade 12 physics

I would say the answer should be -400, since you wouldn't be doing work to get the charge across in that direction, the charge plates would be doing 400 Joules of work though.

Is this the work done by electric field ?

is education illegal in the US?

only works if electric field is constant as in this case of parallel plates.

It's seriously that simple? In Calc 3 currently trying to get prepped for higher level undergrad, and this is what electrical work is? Crazy

Work will be negative. We are not working against the field.

The phrasing "How much work it takes to move an object from point A to point B?" refers to the external work (let's say, you) are required to do in order to make the objects between the two points, such that it begins at rest in point A and finishes at rest in point B. This is important.
Let's say the object is a point mass, and you want to take it from the bottom of a mountain to the top of the mountain. Of course, you gotta put work into it.
But what if you want to bring the mass from the top of the mountain to the bottom? It would have done so by itself anyway if you just nudge it a bit. Instead, you gotta take energy away from the object, in order to make sure it reaches the end and stops instead of keeping on moving. That's why it takes a negative work to get an object off a mountain.
This is essentially true at all scenarios. If the net force in the system (excluding the external force) pushes the body in the direction of it's course, then you gotta oppose it by taking away from the kinetic energy it accumulates. If the net force in the system is opposing the trajectory of the object, then you gotta push it against this work and make it move in the "unnatural" way.
When the net force "helps" the object, the work needed is negative. When it "opposes", the work needed is positive.

Lastly, when asked on a specific force and not "the work needed", then the logic is reversed. In the case above, gravity helps the ball to get out of the mountain and therefore it exerts positive work in that direction. Gravity opposes the object from climbing the mountain, and therefore exerts a negative work in the process.

Bonus question: Imagine you ride a bike or a car. Or even start walking. You start from rest, accelerates, and then move at a constant speed. Obviously, you gained kinetic energy and therefore positive work have been done on you. What force exerted the work? How does it happen?

This “hardest problem taught in college” came in my 12th grade physics paper, and I didn’t find much problem solving it

I am 14 I read already this in a book

Unnecessary bro. E=qV is enough

The integral is with respect to x, Why? Shouldn't it be with respect to t ?

wtf why are we mentioning integrals ☹️ i hate calculus

Without the knowledge of calculus and physics you're in a state reckoning.

Shouldn't the work be negative, as it is done by the system itself and does not require any external work?

My school straight up teaches us the formula

Is it good that I can solve this before being born yet?

The way the question is stated is misleading. One should read :

What is the work of the electric forces on a positive charge q to move it from the 300V to the 100V plate ?

The way it's stated now seems to read as :

What would be the work required to give to the positive charge to move it from one plate to the other AGAINST the electric field in that region of space ?

Which of course is the opposite result of what is discussed in the video.

Making sure to specify the point of view in the questions is essential to avoid any confusion. ;-)

Voltage = Work Done per unit Charge. Hence dW=qdV.... Easy Peesy

People who did it without equation


😑